Fluid
Mechanics and Hydraulic Engineering of Dam Break Wave. From the Dam
Busters to Self-Flowing Concrete Testing
by Hubert CHANSON (h.chanson@uq.edu.au)
M.E., ENSHM Grenoble, INSTN, PhD (Cant.), DEng (Qld),
Eur.Ing., MIEAust., MIAHR, 13th
Arthur Ippen awardee
School of Civil Engrg., Univ. of Queensland, Brisbane QLD
4072, Australia
 Presentation
Presentation
Dam break waves have been responsible for numerous losses of life (e.g. Fig.
1 and 2). Figures 1 and 2 illustrate two tragic accidents : the catastrophes
of the St Francis dam (USA 1928) and of the Malpasset dam (France 1959).
Another situation is the bombing of the Ruhr dams by the "Dam Busters"
during Word War II on 16/17th May 1943 (Fig. 3) (WEBSTER 2005). Figure 3
shows the Mohne dam breach after the bombing. Related situations include
flash flood runoff in ephemeral streams, debris flow surges and tsunami
runup on dry coastal plains. In all cases, the surge front is a sudden
discontinuity characterised by extremely rapid variations of flow depth and
velocity. Dam failures motivated basic studies on dam break wave, including
the milestone contribution by RITTER (1892) following the South Fork
(Johnstown) dam disaster (USA, 1889). Physical modelling of dam break wave
is relatively limited despite a few basic experiments. In retrospect, the
experiments of SCHOKLITSCH (1917) were well ahead of their time, and
demonstrated that Armin von SCHOKLITSCH (1888–1968) had a solid
understanding of both physical modelling and dam break processes.
Theoretical modelling has also been limited despite the oustanding
contributions of DRESSLER (1952) and WHITHAM (1954).
Herein two basic dam break wave applications are reviewed. That is, a new
analytical solution of the dam break wave in a horizontal channel with bed
friction, and the dam break wave motion of a non-Newtonian thxotropic fluid.
Analytical solution of dam break
wave with bed friction
A dam break wave is the flow resulting from a sudden release of a mass of
fluid in a channel. For one-dimensional applications, the continuity and
momentum equations yield the Saint-Venant equations (BARRÉ de SAINT-VENANT
1871a,b). For a frictionless dam break in a wide, horizontal, initially-dry
channel, the analytical solution of the Saint-Venant equations yields Ritter
solution (RITTER 1892). The solution does not however takes into account.
DRESSLER (1952) and WHITHAM (1955) solved analytically the dam break wave
problem with bed friction. A simpler, newer solution was recently developed
(CHANSON 2005).
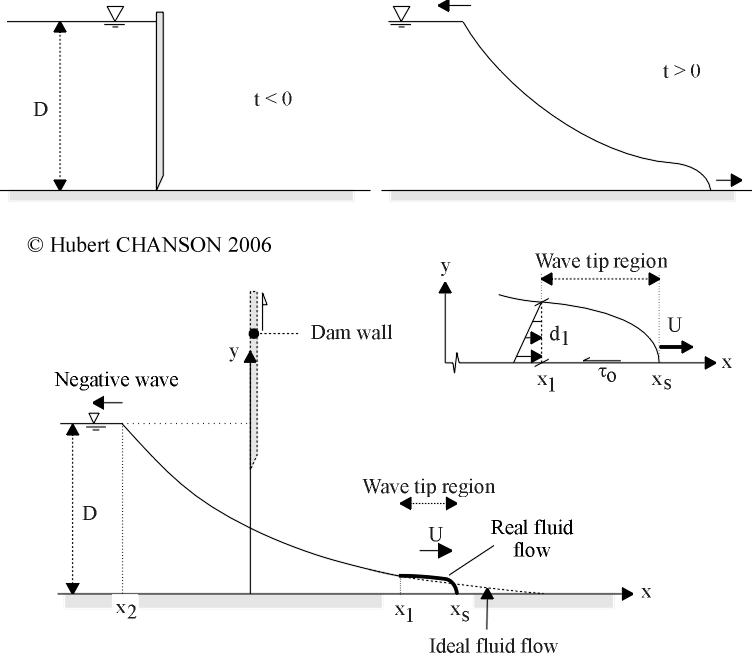
Let us consider an instantaneous dam break in a rectangular, prismatic
channel with bed friction and for a semi-infinite reservoir. The turbulent
dam break flow is analysed as an ideal-fluid flow region behind a flow
resistance-dominated tip zone (Fig. 4). WHITHAM (1955) introduced this
conceptual approach that was used later by other researchers, but these
mathematical developments differ from the present simple solution. In the
wave tip region (x1 < x < xs, Fig. 4), the flow velocity does not vary
rapidly in the wave tip zone. If the flow resistance is dominant, and the
acceleration and inertial terms are small, the dynamic wave equation may be
reduced into a diffusive wave equation (CHANSON 2005).
 Assuming
a
constant Darcy-Weisbach friction factor in the wave-tip region, the exact,
analytical solution is:
Assuming
a
constant Darcy-Weisbach friction factor in the wave-tip region, the exact,
analytical solution is:
(1) 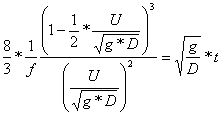
(2) 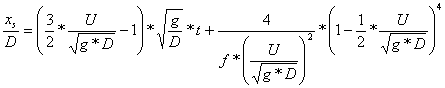
where f is the Darcy-Weisbach friction factor. The instantaneous
free-surface profile is then :
(3) 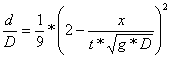 Ideal fluid fow region
Ideal fluid fow region
(4) 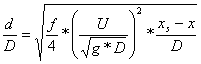 Wave tip, friction-dominated region
Wave tip, friction-dominated region
The analytical solution was compared systematically with several
experimental studies. The comparative analysis suggested that the results
were sensitive to the choice of the Darcy friction factor and that its
selection must be based upon a match with instantaneous free-surface
profiles. Alternate comparisons with wave front celerity or location data
are approximate and often unsuitable.
Ultimately, a practical question is : which is the best theoretical model
for turbulent dam break wave? DRESSLER's (1952) method is robust, but the
treatment of the wave leading edge is approximate : "To
handle the tip region accurately, some type of boundary-layer technique
would be necessary [...] but no results are yet available. [...] In the
absence of more satisfactory boundary layer results, we will apply [...]
approximate considerations to obtain some data about the wavefront"
(DRESSLER 1952, pp. 223-224). WHITHAM's (1955) method is also a robust
technique, but the results are asymptotic solutions. The newer model of
CHANSON (2005) with constant friction factor provides complete explicit
solutions of the entire flow field. The velocity field and water depths are
explicitly calculated everywhere. In practice, the selection of a suitable
analytical model is linked with its main application. For example, for
pedagogical purposes, the writer believes that the above model based upon a
constant friction coefficient in the wave tip region is nicely suited to
introductory courses and young professionals because of the explicit and
linear nature of the results.
Dam break wave of non-Newtonian
thixotropic fluid
In natural mudflows, the interstitial fluid made of clay and water plays a
major role in the rheological behaviour of the complete material. Since
clay-water suspensions have often been considered as thixotropic yield
stress fluids, it is likely that thixotropy plays a role in some cases of
natural events. Thixotropy is the characteristic of a fluid to form a
gelled structure over time when it is not subjected to shearing and to
liquefy when agitated. A thixotropic fluid appears as a non-Newtonian
fluid exhibiting an apparent yield stress and an apparent viscosity that
are functions of both the shear intensity and the current state(s) of
structure of the material. Under constant shear rate, the apparent
viscosity of a thixotropic fluid changes with time until reaching
equilibrium. To date, it is essentially the yielding character of
non-Newtonian fluid behaviour which has been taken into account for
modelling either steady, slow spreading and rapid transient free surface
flows (COUSSOT 1997). There is a need to explore the interplay of the
yielding and thixotropic characters of mud and debris flows. Practical
applications encompass also concrete tests including L-Box and J-Ring for
self-consolidating (superflowing) concrete testing, preparation of
industrial paints, pasty sewage sludges, and some wastewater treatment
residues.
 A recent work described a basic study of dam break
wave with non-Newtonian thixotropic fluid (CHANSON et al. 2006. Such a
highly unsteady flow motion has not been studied to date with thixotropic
fluid, despite its practical applications : e.g., mudflow release,
superflowing concrete flows, preparation of industrial paints. Theoretical
considerations were developed based upon a kinematic wave approximation of
the Saint-Venant equations down a prismatic sloping channel (Fig. 5) and
combined with the thixotropic rheological model of COUSSOT et al. (2002).
Theoretical results highlighedt three different flow regimes depending
upon the initial degree of fluid jamming Tetao and upon the ratio do /hc.
These flow regimes are: (1) a relatively-rapid flow stoppage for
relatively small mass of fluid (do/hc < 1) or large initial rest period
To (i.e. large Lambdao) (Cases A and B1), (2) a fast flow motion for large
mass of fluid (do/hc >> 1) (Case C), and (3) an intermediate motion
initially rapid before final fluid stoppage for intermediate mass of fluid
(do/hc > 1) and intermediate initial rest period To (i.e. Lambdao)
(Cases B2 and B3).
A recent work described a basic study of dam break
wave with non-Newtonian thixotropic fluid (CHANSON et al. 2006. Such a
highly unsteady flow motion has not been studied to date with thixotropic
fluid, despite its practical applications : e.g., mudflow release,
superflowing concrete flows, preparation of industrial paints. Theoretical
considerations were developed based upon a kinematic wave approximation of
the Saint-Venant equations down a prismatic sloping channel (Fig. 5) and
combined with the thixotropic rheological model of COUSSOT et al. (2002).
Theoretical results highlighedt three different flow regimes depending
upon the initial degree of fluid jamming Tetao and upon the ratio do /hc.
These flow regimes are: (1) a relatively-rapid flow stoppage for
relatively small mass of fluid (do/hc < 1) or large initial rest period
To (i.e. large Lambdao) (Cases A and B1), (2) a fast flow motion for large
mass of fluid (do/hc >> 1) (Case C), and (3) an intermediate motion
initially rapid before final fluid stoppage for intermediate mass of fluid
(do/hc > 1) and intermediate initial rest period To (i.e. Lambdao)
(Cases B2 and B3).
The physical observations of flow regimes (Fig. 6) were in remarkable
agreement with theoretical considerations. In particular, exactly the same
flow regimes were identified as well as same trends for the effects of the
bentonite concentration and rest time. For example, theoretical
considerations predict an intermediate motion with initially rapid before
final fluid stoppage for intermediate mass of fluid M (i.e. do/hc > 1)
and intermediate initial rest period To. The theory predicts a faster flow
stoppage with increasing rest period. Similarly, it shows that an increase
in bentonite mass concentration, associated with an increase in the
product (Teta*Alpha), yields a faster fluid stoppage with a larger final
fluid thickness. A similar comparison between theory and physical
experiments may be developed for fast-flowing motion and relatively-rapid
flow stoppage situations. This qualitative agreement between simple theory
and reality means that the basic physical ingredients of the rheological
model and kinematic wave equations are likely to be at the origin of the
observed phenomena. Interestingly the Flow Type III is the only flow
pattern not predicted by theoretical considerations. It is believed that
this reflects simply the limitations of the Saint-Venant equations (1D
flow equations) and of the kinematic wave approximation that implies a
free-surface parallel to the chute invert, hence incompatible with the
Type III free-surface pattern.
Basically the qualitative agreement between the present theory and
experiments with bentonite suspensions (Fig. 6) suggested that the basic
equations of this development (i.e. kinematic wave equation and rheology
model) are likely to model correctly both fluid behaviour and flow motion.
 Detailed
photographs
Detailed
photographs
Figure 1 - St Francis
dam (USA 1928). Photo No. 1 :
view of remnant part after dam collapse. Completed in 1926 near Los Angeles,
the 62.5-m high gravity dam completed in 1926 was equipped with a stepped
spillway (width: 67 m). The dam wall failed on 12 March 1928 because of
foundation failure. More than 450 people died in the catastrophe. (Ref.: CHANSON 1995, Pergamon, pp.
191-193).
Figure 2 - Malpasset dam (Fréjus, France 1959). Photo
No. 1, Photo No. 2 : in Dec. 1981
(taken by H. CHANSON). Completed at the end of 1953, the 102-m high arch dam
(double curvature) had a maximum reservoir capacity of about 50 Mm3. On 2
Dec. 1959, the dam wall failed and more than 450 people died in the
catastroph. The failure was caused by uplift pressures in the rock
foundation (left abutment).
Figure 3 - Ruhr dams and Dam Buster campain (WWII, 1943).
Mohne dam (Germany). Completed in
1913, the curved gravity dam was 650 m long and 40 m high, with a storage
capcity of 134.5 E+6 m3. The dam hit and badly damaged by the "dam busters"
during Word War II on 16/17th May 1943. Almost 1,300 people died in the
floods following the dam buster campaign, mostly inmates of a Prisoner of
War (POW) camp just below the dam. The dam breach was 23 m high and 77 m
long. Photo No. 3.1 : Mohne dam break
damage during the reconstuction in less than 4 months in 1943 (Courtesy of
Ruhrverband, Essen, Germany).
Sorpe dam (Germany) Built between
1926 and 1935, the embankment dam was 69 m high and 700 m long. It was built
with a concrete core. The reservoir storage capacity is 70.8 E+6 m3 for a
catchment area of 100 km2 [extended] (53 km2 [original]). The dam was little
damaged by the "dam buster" campaign. Photo
No. 3.2 : Removal of an unexploded 5-tons 1943 bomb during the Sorpe
dam refurbishment in 1959 (Courtesy of Ruhrverband, Essen, Germany).
Figure 4 - Sketch of a dam break
wave in a horizontal channel with bed friction (after CHANSON
2005)
Figure 5 - Dam break wave down an
inclined channel with bed friction (after CHANSON
et al. 2004)
Figure 6 - Dam break wave of non-Newtonian thixotropic fluid -
Sudden release of bentonite suspension on an inclined plane (15 deg.) (Ref.
CHANSON et al. 2004,
2006). Photo
No. 6.1 : Test 3, 15 deg. slope, 15% bentonite mass concentration, dam
break after 1 minute relaxation, photograph taken after fluid stoppage. Photo No. 6.2 : Test 15, 15 deg. slope,
17% bentonite mass concebtration, dam break after 1 min. relaxation,
photograph taken after fluid stoppage. Photo
No. 6.3 : Test 5, 15 deg. slope, 15% bentonite mass concentration, dam
break after 1 minute relaxation, "roll waves" formed during clean upof the
channel.
Related
links
 References
References
BARRÉ de SAINT-VENANT, A.J.C. (1871a). "Théorie et Equations Générales du
Mouvement Non Permanent des Eaux Courantes." Comptes Rendus des séances de
l'Académie des Sciences, Paris, France, Séance 17 July 1871, Vol. 73, pp.
147-154 (in French).
BARRÉ de SAINT-VENANT, A.J.C. (1871b). "Théorie du Mouvement Non Permanent
des Eaux, avec Application aux Crues de Rivières et à l'Introduction des
Marées dans leur Lit." Comptes Rendus des séances de l'Académie des
Sciences, Paris, France, Vol. 73, No. 4, pp. 237-240 (in French).
CHANSON, H. (2004). "Environmental Hydraulics
of Open Channel Flows." Elsevier Butterworth-Heinemann, Oxford, UK,
483 pages (ISBN 0 7506 6165 8).
CHANSON, H. (2005). "Analytical Solution of Dam Break Wave with Flow
Resistance. Application to Tsunami Surges." Proc.
31th Biennial IAHR Congress, Seoul, Korea, B.H. JUN, S.I. LEE, I.W.
SEO and G.W. CHOI Editors, Theme D1, Paper 0137, pp. 3341-3353 (ISBN 89
87898 24 5). (PDF
Version at EprintsUQ)
CHANSON, H., JARNY, S., and COUSSOT, P. (2006). "Dam Break Wave of
Thixotropic Fluid." Jl of Hyd. Engrg., ASCE, Vol. 132, No. 3, pp. 280-293
(ISSN 0733-9429). (PDF
file at UQeSpace)
COUSSOT, P. (1997). "Mudflow Rheology and Dynamics." IAHR Monograph,
Balkema, The Netherlands.
COUSSOT, P., NGUYEN, A.D., HUYNH, H.T., and BONN, D. (2002). "Avalanche
Behavior in Yield Stress Fluids." Physics Review Letters, Vol. 88, p. 175501
DRESSLER, R.F. (1952). "Hydraulic Resistance Effect upon the Dam-Break
Functions." Jl of Research, Natl. Bureau of Standards, Vol. 49, No. 3, pp.
217-225.
RITTER, A. (1892). "Die Fortpflanzung der Wasserwellen." Vereine Deutscher
Ingenieure Zeitschrift, Vol. 36, No. 2, 33, 13 Aug., pp. 947-954 (in
German).
SCHOKLITSCH, A. (1917). Über Dambruchwellen." Sitzungberichten der
Königliche Akademie der Wissenschaften, Vienna, Vol. 126, Part IIa, pp.
1489-1514.
WEBSTER, T.M. (2005). "The Dam Busters Raid: Success or Sideshow?" Air Power
History, Vol. 52, Summer, pp. 12-25.
WHITHAM, G.B. (1955). "The Effects of Hydraulic Resistance in the Dam-Break
Problem." Proc. Roy. Soc. of London, Ser. A, Vol. 227, pp. 399-407.
Bibliography
CASTRO-ORGAZ, O., and CHANSON, H. (2017). "Ritter's Dry-bed Dam-break Flows:
Positive and Negative Wave Dynamics." Environmental Fluid Mechanics, Vol.
17, No. 4, pp. 665–694 (DOI: 10.1007/s10652-017-9512-5) (ISSN 1567-7419
[Print] 1573-1510 [Online]). (View
only) (PDF
file) (Reprint
at UQeSpace)
CASTRO-ORGAZ, O., and CHANSON, H. (2020). "Undular and broken surges in
dam-break flows: a review of wave breaking strategies in a Boussinesq-type
framework." Environmental Fluid Mechanics, Vol. 20, No. 6, pp.
1383-1416 (DOI: 10.1007/s10652-020-09749-3) (ISSN 1567-7419 [Print]
1573-1510 [Online]). (PDF file) (Preprint at UQeSpace)
CASTRO-ORGAZ, O., and CHANSON, H. (2021). "Comparison between hydrostatic
and total pressure simulations of dam-break flows. Discussion." Journal
of Hydraulic Research, IAHR, Vol. 59, No. 2, pp. 351-354 (DOI:
10.1080/00221686.2020.1780504) (ISSN 0022-1686). (PDF file) (Preprint at UQeSpace)
CAVAILLE, Y. (1965). "Contribution à l'Etude de l'Ecoulement Variable
Accompagnant la Vidange Brusque d'une Retenue." ('Contribution to the Study
of Unsteady Flow Following a Dam Break.') Publ. Scient. et Techn. du
Ministère de l'Air, No. 410, Paris, France, 165 pages (in French).
CHANSON, H. (2004). "Experimental Study of Flash Flood Surges Down a Rough
Sloping Channel." Water Resources
Research, Vol. 40, No. 3, paper W03301, Ref. 10.1029/2003WR002662,
12 pages (ISSN 0043-1397). (PDF
file at UQeSpace) (Download PDF file)
CHANSON, H. (2004). "Unsteady Air-Water Flow Measurements in Sudden Open
Channel Flows." Experiments in Fluids,
Vol. 37, No. 6, pp. 899-909 (ISSN 0723-4864). (PDF
file at UQeSpace) (Download PDF
file)
CHANSON, H. (2005). "Air-Water and Momentum Exchanges in Unsteady Surging
Waters : an Experimental Study." Experimental
Thermal and Fluid Science, Vol. 30, No. 1, pp. 37-47 (ISSN
0894-1777). (Download PDF
file)
CHANSON, H. (2005). "Le Tsunami du 26 Décembre 2004: un Phénomène
Hydraulique d'Ampleur Internationale. Premier Constats." ('The 26 December
2004 Tsunami: a Hydraulic Engineering Phenomenon of International
Significance. First Comments') Jl La Houille Blanche, No. 2, pp. 25-32 (ISSN
0018-6368) (in French). (PDF
Version
at EprintsUQ)
CHANSON, H. (2005). "Applications of the Saint-Venant Equations and Method
of Characteristics to the Dam Break Wave Problem." Report
No. CH55/05, Dept. of Civil Engineering, The University of
Queensland, Brisbane, Australia, May, 135 pages (ISBN 1864997966). (PDF
Version at EprintsUQ)
CHANSON, H. (2006). "Solutions Analytiques de l’Onde de Rupture de Barrage
sur Plan Horizontal et Incliné." ('Analytical Solutions of the Dam Break
Wave Problem on Horizontal and Inclined Inverts.') Jl
La Houille Blanche, No. 3, pp. 76-86 (ISSN 0018-6368) (in French).
(PDF version
at UQeSpace) (PDF
file at EprintsUQ) (Corrected
PDF file at EprintsUQ)
CHANSON, H. (2006). "Analytical Solutions of Laminar and Turbulent Dam Break
Wave." Proc. International Conference on
Fluvial Hydraulics River Flow 2006, Lisbon, Portugal, 6-8 Sept.,
Topic A3, R.M.L. FERREIRA, E.C.T.L. ALVES, J.G.A.B. LEAL, and A.H. CARDOSO
Eds., Balkema Publ., Taylor & Francis Group, London, Vol. 1, pp. 465-474
(ISBN 0 415 40815 6). (PDF
file at UQeSpace) (PDF
version at EprintsUQ)
CHANSON, H. (2006). "Tsunami Surges on Dry Coastal Plains: Application of
Dam Break Wave Equations." Coastal
Engineering Journal, Vol. 48, No. 4, pp. 355-370 (ISSN 0578-5634).
(PDF file at EprintsUQ)
CHANSON, H. (2008). "A Simple Solution of the Laminar Dam Break Wave." Journal of Applied Fluid Mechanics,
Vol. 1, No. 1, pp. 1-10 (DOI: 10.36884/jafm.1.01.11831) (ISSN 1735-3645). (PDF
file at UQeSpace) (PDF
file)
CHANSON, H. (2009). "Application of the Method of Characteristics to the Dam
Break Wave Problem." Journal of Hydraulic
Research, IAHR, Vol. 47, No. 1, pp. 41-49 (DOI:
10.3826/jhr.2009.2865) (ISSN 0022-1686). (PDF
file with errata) (PDF
file at UQeSpace)
CHANSON, H. (2020). "Statistical Analysis Method for Transient Flows - The
Dam-Break Case. Discussion." Journal of Hydraulic Research, IAHR,
Vol. 58, No. 6, pp. 1001-1004 (DOI: 10.1080/00221686.2020.1729266) (ISSN
0022-1686). (PDF
file) (Preprint
at UQeSpace)
CHANSON, H., AOKI, S., and MARUYAMA, M. (2002). "An Experimental Study of
Tsunami Runup on Dry and Wet Horizontal Coastlines." International Journal
of the Tsunami Society, Science of Tsunami Hazards, Vol. 20, No. 5, pp.
278-293 (ISSN 8755-6839). (PDF
Version at EprintsUQ)
CHANSON, H., and COUSSOT, P. (2005). "Fluid Dynamic Treatment of Thixotropic
Debris Flows and Avalanches." Proc. 31th Biennial IAHR Congress, Seoul,
Korea, B.H. JUN, S.I. LEE, I.W. SEO and G.W. CHOI Editors, Theme D.5, Paper
0039, pp. 5654-5666 (ISBN 89 87898 24 5). (PDF
Version at EprintsUQ)
CHANSON, H., COUSSOT, P., JARNY, S., and TOQUER, L. (2004). "A Study of Dam
Break Wave of Thixotropic Fluid: Bentonite Surges down an Inclined Plane."
Report No. CH54/04, Dept. of Civil Engineering, The University of
Queensland, Brisbane, Australia, June, 90 pages (ISBN 1864997710). (PDF
Version at EprintsUQ)
CHANSON, H. JARNY, S., TOCQUER, L., and COUSSOT, P. (2004). "An Experimental
Study of Sudden Release of Bentonite Suspensions down an Inclined Chute."
Proc. 15th Australasian Fluid Mech. Conf., AFMC, Sydney, Australia, M.
BEHNIA, W. LIN & G.D. McBAIN Ed., Paper AFMC00252, 4 pages (CD-ROM)
(ISBN 1-864-87695-6). (PDF
Version at EprintsUQ)
COUSSOT, P., ROUSSEL, N., JARNY, S., and CHANSON, H. (2005). "Continuous or
Catastrophic Solid-Liquid Transition in Jammed Systems." Physics of Fluids,
Vol. 17, No. 1, Article 011703, 4 pages (ISSN 0031-9171). (PDF
Version at EprintsUQ)
DRESSLER, R. (1954). "Comparison of Theories and Experiments for the
Hydraulic Dam-Break Wave." Proc. Intl Assoc. of Scientific Hydrology
Assemblée Générale, Rome, Italy, Vol. 3, No. 38, pp. 319-328.
ESTRADE, J. (1967). "Contribution à l'Etude de la Suppression d'un Barrage.
Phase Initiale de l'Ecoulement." ('Contribution to the Study of Dam Break.
Initial Stages of the Wave.') Bulletin de la Direction des Etudes et
Recherches, Series A, Nucléaire, Hydraulique et Thermique, EDF Chatou,
France, No. 1, pp. 3-128.
Video movie
Dam break wave, Tidal bore, In-river tsunami surge: what the hell? - - {https://youtu.be/SQaPoSj2lP4} (Record
at UQeSpace) (UQ
Civil Engineering YouTube channel)
Acknowledgments
The writer acknowledges the asssitance of Dr P. COUSSOT (LMSGC).
License

This work is licensed under a Creative
Commons Attribution-NonCommercial 3.0 Unported License.
Hubert
CHANSON is a Professor in Civil Engineering, Hydraulic Engineering
and Environmental Fluid Mechanics at the University
of Queensland, Australia. His research interests include design of
hydraulic structures, experimental investigations of two-phase flows,
applied hydrodynamics, hydraulic engineering, water quality modelling,
environmental fluid mechanics, estuarine processes and natural resources.
He has been an active consultant for both governmental agencies and
private organisations. His publication record includes over 950
international refereed papers and his work was cited over 6,000 times
(WoS) to 22,500 times (Google
Scholar) since 1990. His h-index is 43 (WoS), 45 (Scopus) and 75 (Google
Scholar), and he is ranked among the 150 most cited researchers in
civil engineering in Shanghai’s
Global Ranking of Academics. Hubert Chanson is the author of twenty
books, including "Hydraulic Design
of Stepped Cascades, Channels, Weirs and Spillways" (Pergamon,
1995), "Air Bubble Entrainment in
Free-Surface Turbulent Shear Flows" (Academic
Press, 1997), "The Hydraulics
of Open Channel Flow : An Introduction" (Butterworth-Heinemann,
1st edition 1999, 2nd
editon 2004), "The Hydraulics of
Stepped Chutes and Spillways" (Balkema,
2001), "Environmental
Hydraulics of Open Channel Flows" (Butterworth-Heinemann,
2004), "Tidal
Bores, Aegir, Eagre, Mascaret, Pororoca: Theory And Observations" (World
Scientific, 2011) and "Applied
Hydrodynamics:
an Introduction" (CRC
Press, 2014). He co-authored three further books "Fluid Mechanics
for Ecologists" (IPC Press, 2002), "Fluid Mechanics for Ecologists.
Student Edition" (IPC, 2006) and
"Fish Swimming in Turbulent Waters. Hydraulics Guidelines
to assist Upstream Fish Passage in Box Culverts" (CRC Press 2021). His textbook "The Hydraulics
of Open Channel Flows : An Introduction" has already been translated
into Spanish (McGraw-Hill
Interamericana) and Chinese (Hydrology Bureau of Yellow
River Conservancy Committee), and the second
edition was published in 2004. In 2003, the IAHR
presented him with the 13th Arthur Ippen Award
for outstanding achievements in hydraulic engineering. The American
Society of Civil Engineers, Environmental and Water Resources Institute
(ASCE-EWRI) presented him with the 2004 award for the Best Practice paper
in the Journal of Irrigation and Drainage Engineering ("Energy
Dissipation
and Air Entrainment in Stepped Storm Waterway" by Chanson and
Toombes 2002) and the 2018 Honorable Mention Paper Award for "Minimum Specific
Energy and Transcritical Flow in Unsteady Open-Channel Flow" by
Castro-Orgaz and Chanson (2016) in the ASCE Journal of Irrigation and
Drainage Engineering. The Institution of Civil Engineers (UK) presented
him the 2018 Baker Medal. In 2018, he was inducted a Fellow of the Australasian Fluid Mechanics Society.
Hubert Chanson edited further several books : "Fluvial,
Environmental and Coastal Developments in Hydraulic Engineering"
(Mossa, Yasuda & Chanson 2004, Balkema),
"Hydraulics.
The
Next Wave" (Chanson & Macintosh 2004, Engineers
Australia), "Hydraulic
Structures:
a Challenge to Engineers and Researchers" (Matos & Chanson 2006,
The University of Queensland), "Experiences and
Challenges in Sewers: Measurements and Hydrodynamics" (Larrate &
Chanson 2008, The University of
Queensland), "Hydraulic
Structures:
Useful Water Harvesting Systems or Relics?" (Janssen & Chanson
2010, The University of Queensland),
"Balance
and Uncertainty: Water in a Changing World" (Valentine et al. 2011,
Engineers Australia), "Hydraulic
Structures and Society – Engineering Challenges and Extremes"
(Chanson and Toombes 2014, University
of Queensland), "Energy
Dissipation
in Hydraulic Structures" (Chanson 2015, IAHR
Monograph, CRC Press). He chaired the Organisation of the 34th
IAHR World Congress held in Brisbane, Australia between 26 June and
1 July 2011. He chaired the Scientific Committee of the 5th IAHR
International Symposium on Hydraulic Structures held in Brisbane in
June 2014. He chaired the Organisation of the 22nd Australasian Fluid
Mechanics Conference in Brisbane, Australia on 6-10 December 2020.
His Internet home page is http://www.uq.edu.au/~e2hchans.
He also developed a gallery of photographs website {http://www.uq.edu.au/~e2hchans/photo.html}
that received more than 2,000 hits per month since inception.
More pictures of self-aeration are here
...
TECHNICAL INTERNET RESOURCES
More about a history of arch dams
... More about timber crib
weirs ... More about steel
dams ...
More about engineering
failures ... More about rubber
dams ... More about a tidal
bore ...
More about the Formal Water Garden
.... More about rapid
reservoir sedimentation in Australia ...
More about Minimum Energy Loss culverts
.. More about Minimum Energy
Loss weirs ...
This page was visited : 5,835 times between
18-03-2006 and June 2012.
Last updated on 27/03/2022










 A recent work described a basic study of dam break
wave with non-Newtonian thixotropic fluid (CHANSON et al. 2006. Such a
highly unsteady flow motion has not been studied to date with thixotropic
fluid, despite its practical applications : e.g., mudflow release,
superflowing concrete flows, preparation of industrial paints. Theoretical
considerations were developed based upon a kinematic wave approximation of
the Saint-Venant equations down a prismatic sloping channel (Fig. 5) and
combined with the thixotropic rheological model of COUSSOT et al. (2002).
Theoretical results highlighedt three different flow regimes depending
upon the initial degree of fluid jamming Tetao and upon the ratio do /hc.
These flow regimes are: (1) a relatively-rapid flow stoppage for
relatively small mass of fluid (do/hc < 1) or large initial rest period
To (i.e. large Lambdao) (Cases A and B1), (2) a fast flow motion for large
mass of fluid (do/hc >> 1) (Case C), and (3) an intermediate motion
initially rapid before final fluid stoppage for intermediate mass of fluid
(do/hc > 1) and intermediate initial rest period To (i.e. Lambdao)
(Cases B2 and B3).
A recent work described a basic study of dam break
wave with non-Newtonian thixotropic fluid (CHANSON et al. 2006. Such a
highly unsteady flow motion has not been studied to date with thixotropic
fluid, despite its practical applications : e.g., mudflow release,
superflowing concrete flows, preparation of industrial paints. Theoretical
considerations were developed based upon a kinematic wave approximation of
the Saint-Venant equations down a prismatic sloping channel (Fig. 5) and
combined with the thixotropic rheological model of COUSSOT et al. (2002).
Theoretical results highlighedt three different flow regimes depending
upon the initial degree of fluid jamming Tetao and upon the ratio do /hc.
These flow regimes are: (1) a relatively-rapid flow stoppage for
relatively small mass of fluid (do/hc < 1) or large initial rest period
To (i.e. large Lambdao) (Cases A and B1), (2) a fast flow motion for large
mass of fluid (do/hc >> 1) (Case C), and (3) an intermediate motion
initially rapid before final fluid stoppage for intermediate mass of fluid
(do/hc > 1) and intermediate initial rest period To (i.e. Lambdao)
(Cases B2 and B3).  Presentation
Presentation  Assuming
a
constant Darcy-Weisbach friction factor in the wave-tip region, the exact,
analytical solution is:
Assuming
a
constant Darcy-Weisbach friction factor in the wave-tip region, the exact,
analytical solution is: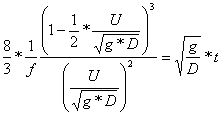
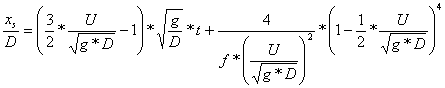
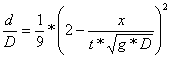 Ideal fluid fow region
Ideal fluid fow region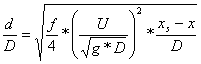 Wave tip, friction-dominated region
Wave tip, friction-dominated region Detailed
photographs
Detailed
photographs References
References












